Пример 1. В остроугольном треугольнике ABC проведена высота BH, <BAC=37°. Найдите угол.

Т.к. треугольник ABH - прямоугольный (BH - высота), то сумма острых углов треугольника равна 90 градусов:

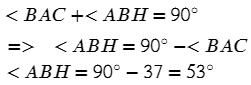
Ответ: 53

Пример 2. В треугольнике ABC угол С равен 142°. Найдите внешний угол при вершине С. Ответ дайте в градусах.

т.к. один из углов треугольника равен 142 градуса, значит он тупоугольный.

Угол называется тупым, если его градусная мера больше 90 градусов.

Треугольник называется тупоугольным если имеет тупой угол.

Внешний угол треугольника - это угол треугольника смежный с внутренним углом при той же вершине.

Смежные углы треугольника в сумме дают 180 градусов:

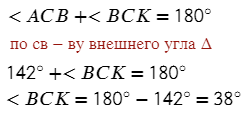
Ответ: 38

Пример 3. Один из углов равнобедренной трапеции равен 66°. Найдите больший угол этой трапеции. Ответ дайте в градусах.

Угол, градусная мера которого меньше 90 градусов называется острым.

В равнобедренной трапеции углы при основании равны: <A=<D,  <B=<C.

Угол в 66 градусов - острый угол, трапеция равнобедренная, следовательно в нашей трапеции это углы А и D.

Трапеция - это четырехугольник у которого две противоположные стороны параллельны, а две другие нет.

Поэтому рассмотрим один из признаков параллельности прямых (отрезков): если две прямые параллельны, то односторонние углы в сумме составляют 180 градусов.

Углы A и B - односторонние, BC параллельно AD, значит:

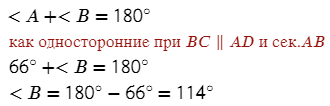
Ответ: 114

Пример 4. Один из углов прямоугольной трапеции равен 64°. Найдите больший угол этой трапеции. Ответ дайте в градусах.

Трапеция называется прямоугольной, если у нее два угла прямые.

Угол, градусная мера которого меньше 90 градусов называется острым.

Угол в 64 градуса - острый угол, трапеция прямоугольная, следовательно в нашей трапеции это угол D.

Трапеция - это четырехугольник у которого две противоположные стороны параллельны, а две другие нет.

Поэтому рассмотрим один из признаков параллельности прямых (отрезков): если две прямые параллельны, то односторонние углы в сумме составляют 180 градусов.

Углы C и D - односторонние, BC параллельно AD, значит:

Ответ: 116

Пример 5. Один из углов параллелограмма равен 41°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.

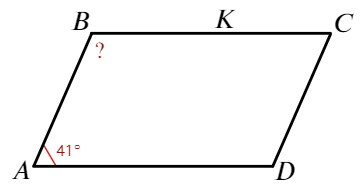
В параллелограмме противоположные углы равны: <A=<C, <B=<D.

Угол, градусная мера которого меньше 90 градусов называется острым.

Угол в 41 градус - острый угол, следовательно это углы A и D.

Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны.

Поэтому рассмотрим один из признаков параллельности прямых (отрезков): если две прямые параллельны, то односторонние углы в сумме составляют 180 градусов.

Углы A и B - односторонние, BC параллельно AD, значит:

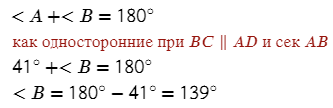
Ответ: 139

Пример 6. Один из углов ромба равен 43°. Найдите больший угол этого ромба. Ответ дайте в градусах.

В ромбе противоположные углы равны: <A=<C, <B=<D.

Угол, градусная мера которого меньше 90 градусов называется острым.

Угол в 43 градуса - острый угол, следовательно в нашем ромбе это углы A и C.

Ромб - это параллелограмм с равными сторонами. Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны.

Поэтому рассмотрим один из признаков параллельности прямых (отрезков): если две прямые параллельны, то односторонние углы в сумме составляют 180 градусов.

Углы A и B - односторонние, BC параллельно AD, значит:

Ответ: 137

Пример 7. В ромбе ABCD угол ABC равен 72°. Найдите угол ACD. Ответ дайте в градусах.

В ромбе противоположные углы равны: <A=<C, <B=<D.

Угол, градусная мера которого меньше 90 градусов называется острым.

Угол в 72 градуса - острый угол, следовательно в нашем ромбе это углы B и D.

Ромб - это параллелограмм с равными сторонами. Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны.

Поэтому рассмотрим один из признаков параллельности прямых (отрезков): если две прямые параллельны, то односторонние углы в сумме составляют 180 градусов.

Углы B и C - односторонние, CD параллельно AB, значит:

Диагонали робма являются биссектрисами соответствующих углов (свойство ромба).

Ответ: 54

Пример 8. В треугольнике два угла равны 57° и 86°. Найдите его третий угол. Ответ дайте в градусах.

Сумма углов любого треугольника равна 180 градусов.

Ответ: 37

Пример 9. Один из острых углов прямоугольного треугольника равен 34°. Найдите его другой острый угол. Ответ дайте в градусах.

Сумма острых углов прямоугольного треугольника равна 90 градусов.

Треугольник называется прямоугольным, если у него есть прямой угол (угол в 90 градусов).

Ответ: 56

Пример 10. В треугольнике ABC известно, что AB = BC, ∠ABC = 108°. Найдите угол BCA. Ответ дайте в градусах.

Треугольник называется равнобедренным, если у него две боковые стороны равны, и два угла при основании равны.

Ответ: 36

Пример 11. Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 66° и 1° соответственно. Ответ дайте в градусах.

Трапеция называется равнобедренной, если две ее боковые стороны равны, а следовательно и углы при основании равны: <A=<D, <B=C.

Трапеция - это четырехугольник у которого две противоположные стороны параллельны, а две другие нет.

Поэтому рассмотрим один из признаков параллельности прямых (отрезков): если две прямые параллельны, то односторонние углы в сумме составляют 180 градусов.

Углы A и B - односторонние, BC параллельно AD.

Ответ: 113

Пример 12. В трапеции ABCD известно, что AB=CD, <BDA=35° и <BDC=58°. Найдите угол ABD. Ответ дайте в градусах.

Ответ: 52

Пример 13. Сумма двух углов равнобедренной трапеции равна 50°. Найдите больший угол этой трапеции. Ответ дайте в градусах.

Ответ: 88

Пример 14. Диагональ прямоугольника образует угол 50° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

Решается аналогично предыдущей.

Ответ: 80