Пример 1Пример 2Пример 3Пример 4Пример 5Пример 6Пример 7Пример 8
Задания этого типа ориентированы на знание основ тригонометрии.
Чтобы справиться с тренажером, необходимо повторить такие темы как: определение тригонометрических функций через прямоугольный треугольник, основное тригонометрическое тождество, а так же необходимо знать как выразить тангенс угла через синус и косинус.
В треугольнике ABC угол С равен 90°, AC=1, AB=5. Найдите sinB.
<strong>Решение</strong>
Треугольник ABC – прямоугольный, т.к. <C=90°
BC и AC – катеты, AB – гипотенуза.
Синус угла прямоугольного треугольника равен отношению противолежащего угла к гипотенузе.
Ответ: 0,2
В треугольнике ABC угол С равен 90°, BC=8, AB=10. Найдите cosB.
Решение
Треугольник ABC – прямоугольный, т.к. <C=90°
BC и AC – катеты, AB – гипотенуза.
Косинус угла прямоугольного треугольника равна отношению прилежащего катета к гипотенузе.
Ответ: 0,4
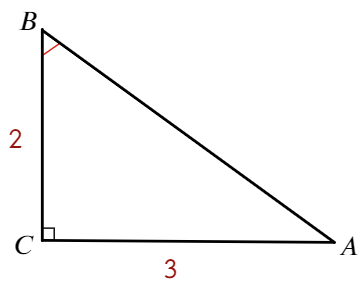
В треугольнике ABC угол С равен 90°, BC=5, AC=2. Найдите tgB.
Решение
Треугольник ABC – прямоугольный, т.к. <C=90°
BC и AC – катеты, AB – гипотенуза.
Тангенс угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему.
Ответ: 0,4
В треугольнике ABC угол С равен 90°, sinB=3/7, AB=21. Найдите AC.
Решение
Треугольник ABC – прямоугольный, т.к. <C=90°
BC и AC – катеты, AB – гипотенуза.
Синус угла прямоугольного треугольника равен отношению противолежащего угла к гипотенузе.
Ответ: 9
В треугольнике ABC угол С равен 90°, cosB=2/5, AB=10. Найдите BC.
Решение
Треугольник ABC – прямоугольный, т.к. <C=90°
BC и AC – катеты, AB – гипотенуза.
Косинус угла прямоугольного треугольника равна отношению прилежащего катета к гипотенузе.
Ответ: 4
В треугольнике ABC угол С равен 90°, tgb=3/4, BC=12. Найдите AC.
Решение
Треугольник ABC – прямоугольный, т.к. <C=90°
BC и AC – катеты, AB – гипотенуза.
Тангенс угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему.
Ответ: 9
Синус острого угла A треугольника ABC указан на рисунке. Найдите cosA.
Решение
Если мы знаем синус угла прямоугольного треугольника, то всегда можем найти косинус этого же угла прямоугольного треугольника с помощью основного тригонометрического тождества.
Ответ: 0,4
Косинус острого угла A треугольника ABC указан на рисунке. Найдите sinA.
Решение
Если мы знаем косинус угла прямоугольного треугольника, то всегда можем найти синус этого же угла прямоугольного треугольника с помощью основного тригонометрического тождества.
Ответ: 0,5
Пример 9. В треугольнике ABC известно, что AB=6, BC=12, синус угла указан на рисунке. Найдите площадь треугольника ABC.
Площадь треугольника равна половине произведения боковых сторон на синус угла между ними.
Ответ: 9